Why is a honeycomb hexagonal, and how can that help me? How can I make a curved tensile surface like a roof with minimum tension? How can you make a structure stronger yet lighter than reinforced concrete?
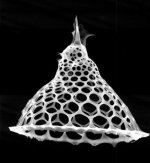 Stick around, I’ll answer these questions, increase your designer’s toolbox, and even tell you how to make one of these guys (radiolaria) on the left here.
Stick around, I’ll answer these questions, increase your designer’s toolbox, and even tell you how to make one of these guys (radiolaria) on the left here.
In the previous article, I asked the reader to consider a spherical raindrop. Indeed, as long as external forces do not impose upon water – gravity, air friction, sides of a container, etc. – it takes a spherical shape. But why?
Water has cohesion, which is a fancy way of saying that it is attracted to itself. To look at it another way, it is sticky to itself. When was the last time you saw the ocean just spontaneously break apart from itself into individual small droplets or a vapour? Liquids just don’t do that. The internal forces – the positive and negative charges on either end of a water molecule – hold the water together.
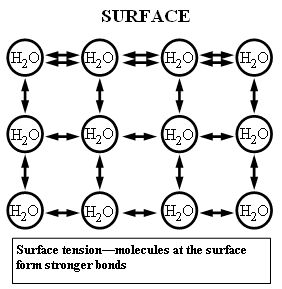
Within the drop, there are attractive forces all around an individual molecule. On the surface, however, there are no atoms outside the drop to attract the surface atoms. This creates a tighter bond amongst the surface atoms, which in turn is what is responsible for surface tension. In water, the surface tension is strong enough that your friendly neighbourhood water strider is able to glide across the surface of water like some sort of Gerridae messiah.
Because the surface molecules are all pulling equally around the entire surface of the droplet, it forms the only shape that equal force would allow, which is a sphere. As hard as you might try to push the droplet into a dodecahedron, as soon as you remove the force, it will snap back into a sphere.
You might wonder what all this has to do with honeybees. Don’t worry, I’m getting to that part. But first, we must look at bubbles. We’ve done half the work already, though. We can consider bubbles to just be anti-drops of water, only instead of water on the inside, we have water on the outside. The key is still the surface tension where air meets liquid.
And before we look at bubbles, we need to look at how they are made. Soap helps us make bubbles because soap molecules are amphiphiles ( meaning “likes both,” often called surfacants), which are molecules with a polar head and a non polar tail. The polar head is attracted to water, which is a polar molecule. The non-polar tail – which is the end sticking out on a bubble – is attracted to non-polar molecules like oil. This reduces the surface tension, which, counter-intuitively, perhaps, makes the bubble more resilient. (This property of being an amphiphile also lets us clean greasy dishes. The soap molecules are attracted to the oil at the non-polar end, surrounding them, and the polar end lets the water carry it.)
You’ve seen two bubbles meet before. They form a plane between them with the dividing bubble wall being just as thick as the wall of a single bubble. Even though two bubbles meet, the wall is not twice as thick. Maintaining that thickness would require more energy. Things naturally seek the lowest energy state, however, so the surplus soapy liquid distributes across the whole surface area of the two bubbles. They also join in a way that minimizes the surface area with respect to their internal pressure.
A light just went off in designer’s heads here. The bubbles form a stable shape with minimum use of material. And this is more than just interesting theory. This aspect of surface tension has been put into design as we shall soon see.
On to the honeycomb! If we take three equal-sized bubbles and touch them together, they will meet with an angle of 120° between the walls. A honeycomb is made up of hexagons, with each point of the hexagon being the centre by which three hexagons touch. There are six points in a hexagon, and six such nexuses around each cell.
It just so happens that there are only three equal-sided shapes that will stack into a plane without leaving gaps: equilateral triangles, squares, and hexagons. Humans tend to like the square because it is simpler to understand. Nature, on the other hand, only knows the principle of minimum energy. So when it comes time to stack round things tightly nature makes the honeycomb rather than the side-by-side stacking in a case of beer (time to redesign beer cases). So when you want to maximize the use of space, for example when planting, you have to mimic the pattern in nature and use a hexagonal array.

Hexagonal planting arrays. Some people are really serious about
getting them right. From
http://www.growbiointensive.org/
Going Deeper
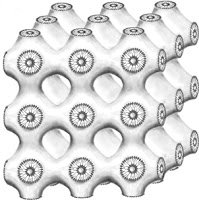
Because of cohesion, the surfacants inside a solution can join together, and do so in some really interesting shapes. One of the shapes that can arise is what’s called the cubic P-phase. Because of the minimum energy principle, this is a shape whose surface tension holds it stable. The entire array is curved, but the total surface curvature adds up to zero.
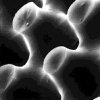 We see this form when we take a look at the skeleton of a sea urchin. This form is stronger than reenforced concrete, giving it promise as a design feature for structures where lightweight strength would be needed.
We see this form when we take a look at the skeleton of a sea urchin. This form is stronger than reenforced concrete, giving it promise as a design feature for structures where lightweight strength would be needed.
Now, I had promised to tell you how to make a radiolarian. Here’s what you don’t do. You don’t try to write some sophisticated genetic code (sorry geneticists) to synthesize proteins that are going to construct these elaborate shapes… somehow. You just write a genetic code for a little guy to blow a foam of bubbles, then inject a mineral in a slurry and allow it to precipitate between the borders of the bubbles. Presto! Marine biologists everywhere will marvel at your intricate beauty!
For our next instalment, we’ll have a little look at an interesting property of surfactants that yields intricate, tightly packed, non-repeating patterns.


Leave a Reply