Update: The Mark III Swale Calculator is here!
Video tutorial:
| Surface | Percentage of runoff |
|---|---|
| Paving, roofs, hard surfaces | 85 to 95% |
| Hardpan | 50 to 70% |
| Bare earth | 20 to 75% |
| Grass | 10 to 25% |
Welcome to the Mark III online permaculture swale spacing calculator. Swale spacing has been a perennial question in permaculture. This calculator creates a template for swale placement based on a logarithmic distribution. It is based on the fact that groundwater flows downward, leaving the top half of hills drier than the bottom. The idea is that water collection should be more intensive at the top of a hill, and be progressively less as you move down the hill.
Why calculate spacing?
Installing swales costs time, energy, and money. Over-installation of swales is a waste of resources. Under-installation is a missed opportunity. If you want to have an optimal system, you’ll need to calculate spacing. The good news is that now it’s easy with our calculator!
How to use this calculator
- You will need to measure the hill from the bottom to the top (or from the bottom accessible boundary to the top accessible boundary, if you hit either physical boundaries or property boundaries). This figure will need to be in metres for the calculator. You can convert units using Google. If you are using an aerial map and are only using the horizontal distance from the bird’s-eye perspective, you will need to convert this to the on-the-ground distance (i.e. the hypotenuse) using trigonometry. (Distance on ground = x ÷ cos Θ where x is the horizontal distance, and Θ is the slope of the hill in degrees.)
- Check the local weather records to see how much rain you can expect in a single large rainfall.
- Input the length of the swale you will build.
- Estimate the slope of the land above the swale in degrees. A mobile app such as Theodolite HD can help here.
- Estimate the percentage of runoff on the site. Use the table above to help you. [Note: If it’s 0%, you can only dig circular swales.]
- Keep in mind that because contour lines are not parallel, the swale spacing will not be uniform across the entire length of the swales. This calculator gives you the best approximation. I do have the the Mark IV in the concept stage, which will address this issue.
- The calculator will return each swale’s location form the bottom of the hill, the volume of each swale, and the cross-sectional area of the swale, which you can use to plan the size of the swale.
- Because of the assumptions built into this calculator, you will need to determine if the volume and cross-sectional area of the top swale is correct or not. You will need to know the catchment area above your swale, and make sure it is big enough to hold all the runoff it will receive.
How spacing works
This calculator assumes you want to capture the maximum amount of water available on a site. There are plenty of times where you will not want to do this. Make sure you know whether swales are going to be helpful or harmful. See An Introduction to Swales and When Swales Can Kill for more information.
Remember that the figures given by the calculator are a guide. There will be an inherent margin of error. Spacing is based off the assumptions that your contour lines are going to be roughly parallel (they won’t be in the real world), and that your catchment area is going to be rectangular in shape (or at least an area with parallel edges). In practice, you might face an irregularly shaped catchment area. The calculator can still serve as a rough guide for you in these instances.
Designing your swale layout
With implementation of earthworks, it is ideal to start at the top and work your way downhill. When designing your plan with this calculator, the figures given (Swale 1, Swale 2, Swale 3, etc.) are from the bottom of the hill to the top. In other words, the first distance for Swale 1 is measured from the bottom of your hill.
Spacing is determined by a logarithmic distribution from bottom to top. This will result in larger, wider spaced swales at the bottom, and closer, smaller swales at the top.
This arrangement makes the most sense in terms of encouraging water infiltration. The water table will drain downward, leaving the top drier. A greater number of swales at the top will allow more water to infiltrate there.
Limitations of the calculator
The question of swale spacing has been an ongoing puzzle in permaculture. A few years ago, it seemed like we had an answer. In Brad Lancaster’s excellent book Rainwater Harvesting for Drylands and Beyond, there is a formula for spacing which in turn cites The Handbook of Hydrology, edited by David Maidment. Unfortunately, the spacing formula isn’t designed to maximize water collection. It gives unit swale volume divided by unit runoff. The problem here is the formula does not take into account the catchment size for the swale. It could have you putting undersized swales at intervals that are not based on the amount of water they will receive. (Testing with the first iteration of this calculator showed this flaw early on.)
The first publicly available online calculator (the Mark II) based spacing on the volume of the swales you built. The problem here is that it did not tell users how to distribute swales across the landscape. This new version provides you will spacing, volume, and cross-sectional area with the minimal amount of input data. That is to say, it does a better job of telling you what to do.
This calculator could be a lot more complicated than it is. It is meant to serve as a good guide to swale design so that you can effectively catch the available runoff without overkill (i.e. without spending more time, money, and effort than you need to spend). It simplifies infiltration rates as a function of runoff. Also, it does not account for hydraulic conductivity (saturated or otherwise), depth to a restrictive layer, and so on. At the end of the day, we are digging a ditch on contour, not launching a spacecraft. Hyper-precision will be a waste of time. It also errs on the side of caution. The volume of your swales at the end does not account for infiltration. This will build some resiliency into your swales. They are better being a little too big than too small.
Behind the scenes
If you want to know what’s going on inside the calculator (and hopefully spot any glaring errors, if there are any), here’s how it works.
- Spacing is determined using log(n+2), where n is the number of swales you select. For a case with 5 swales on a site (i.e. n = 5), we get the distribution shown in the diagram below.
- The runoff above every swale but the top one will be given by the formula: Runoff Volume (litres) = C • ACatchment (m2) • Vrain (mm), where C = Coefficient of Runoff (which is percent runoff ÷ 100), ACatchment is the area of the catchment in m2, Vrain is the volume of a large rain event in mm, and the ACatchment is the Swale Length in metres • Distance to uphill swale in metres.
- Vswale = Runoff Volume
- And Area of swale = Vswale ÷ (Length of swale • 1000). The division by 1000 here is to get us back in the correct units.
This is version 2.0 of this calculator. (But Mark III sounds cooler.)

We’ve got many courses currently in the works and updates to the site, including this page, coming. If you would like to be notified of our updates and courses, subscribe to our mailing list.

 What a summer! Hot and dry, followed by hot and dry periods, interspersed with the promise of thunderstorms that bring furious, desiccating winds, and nothing else.
What a summer! Hot and dry, followed by hot and dry periods, interspersed with the promise of thunderstorms that bring furious, desiccating winds, and nothing else.

 Industrial activity and industrial agriculture consume large amounts of the water that is available. And predictions for continental inlands forecast that global warming will bring drier conditions than those that currently exist. Of the total land mass of the Earth, 47.2% is arid, much of that converted to desert by human activity with a further 25% of the land at risk of desertification. And this problem is not limited to poor nations. While 66% of African lands suffer from desertification, 40% of the pastureland in Texas is now too arid for use. And pivot irrigation is turning patches of land on the Great Plains of North America into salted desert in 3 to 4 years. Even former patches of the Amazon rainforest are very close to becoming desert. Global water consumption is rising so fast that by 2025 demand will surpass availability by 56%. We need to shift to sustainable water usage, or we risk creating a planet largely comprised of desert.
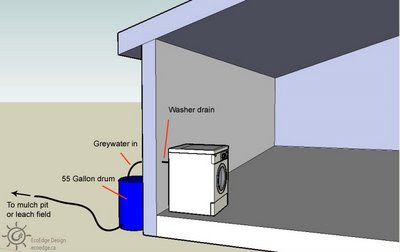
Industrial activity and industrial agriculture consume large amounts of the water that is available. And predictions for continental inlands forecast that global warming will bring drier conditions than those that currently exist. Of the total land mass of the Earth, 47.2% is arid, much of that converted to desert by human activity with a further 25% of the land at risk of desertification. And this problem is not limited to poor nations. While 66% of African lands suffer from desertification, 40% of the pastureland in Texas is now too arid for use. And pivot irrigation is turning patches of land on the Great Plains of North America into salted desert in 3 to 4 years. Even former patches of the Amazon rainforest are very close to becoming desert. Global water consumption is rising so fast that by 2025 demand will surpass availability by 56%. We need to shift to sustainable water usage, or we risk creating a planet largely comprised of desert. Many building codes have a lot of catching up to do when it comes to greywater. A system can be built with a diverter to the currently approved (i.e. unsustainable) system. The diverter can then be used to flow water into the greywater system once the code changes. This system can also be used to deal with freezing conditions mentioned above.
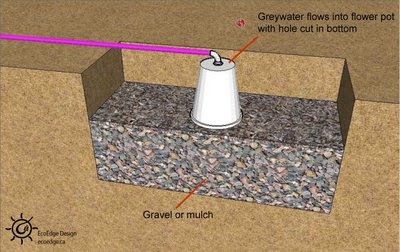
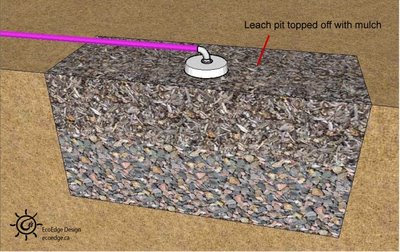
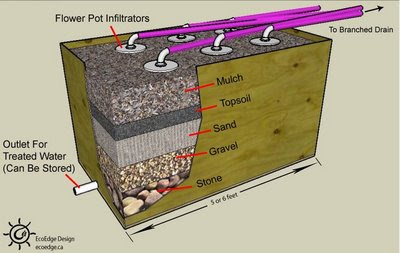
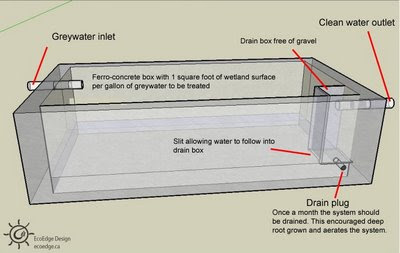
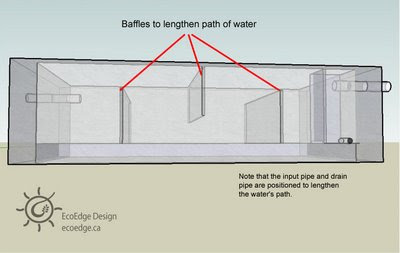
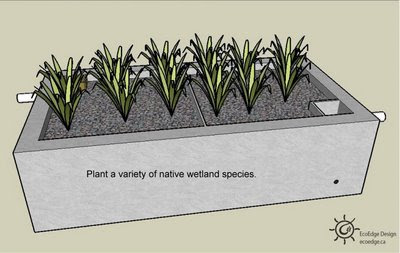
Many building codes have a lot of catching up to do when it comes to greywater. A system can be built with a diverter to the currently approved (i.e. unsustainable) system. The diverter can then be used to flow water into the greywater system once the code changes. This system can also be used to deal with freezing conditions mentioned above. An effective, safe greywater system slowly filters water through the soil so that microbes can devour the organic material in the water. The system should be designed such that people never come in contact with the greywater. The systems can be used to assist food production, provided that the plants are not root crops. Don’t spray grey water on plants (or anything else). The water could contaminate the plant and contaminated water droplets could be inhaled.
An effective, safe greywater system slowly filters water through the soil so that microbes can devour the organic material in the water. The system should be designed such that people never come in contact with the greywater. The systems can be used to assist food production, provided that the plants are not root crops. Don’t spray grey water on plants (or anything else). The water could contaminate the plant and contaminated water droplets could be inhaled.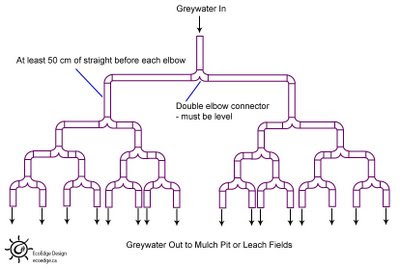 The elbow will effectively halve the flow, but you will need to ensure that the pipe leading up to the elbow has at least 50 cm (about 20”) of straight section. Also, the slope of the pipes should be kept at a fall of 1:48 or steeper to keep the water flowing.
The elbow will effectively halve the flow, but you will need to ensure that the pipe leading up to the elbow has at least 50 cm (about 20”) of straight section. Also, the slope of the pipes should be kept at a fall of 1:48 or steeper to keep the water flowing.